Tehát arra kérték Önt, hogy számítsa ki az eltérést Excel használatával, de nem tudja, hogy ez mit jelent, és nem tudja, hogyan kell ezt megtenni. Ne aggódjon, ez egy egyszerű koncepció és még könnyebb folyamat. Rövid időn belül a variance profi leszel!
Mi az a Variancia?
A „variance” az átlagtól mért átlagos távolság mérésének módja. Az „átlag” az adatkészletben lévő összes érték összege osztva az értékek számával. A variancia képet ad arról, hogy az adott adatkészletben lévő értékek átlagosan egyenletesen tapadnak-e az átlaghoz, vagy szétszóródnak az egész helyen.

Matematikailag a variancia nem olyan összetett:
- Számítsa ki egy értékhalmaz átlagát! Az átlag kiszámításához vegye az összes érték összegét elosztva az értékek számával.
- Vegyél minden értéket a halmazodból, és vond ki az átlagból.
- A kapott értékeket négyzetre emelje (a negatív számok kiküszöböléséhez).
- Adja össze az összes négyzetes értéket.
- Számítsa ki a négyzetes értékek átlagát, hogy megkapja a szórást.
Tehát amint látja, nem nehéz kiszámítani az értéket. Ha azonban több száz vagy ezer értékkel rendelkezik, a manuális elvégzése örökké tart. Szóval jó dolog, hogy az Excel automatizálni tudja a folyamatot!
Mire használod a szórást?
A variancia önmagában számos felhasználási területtel rendelkezik. Pusztán statisztikai szempontból ez egy jó gyorsított módja annak kifejezésére, hogy egy adott adatkészlet mennyire szétszórt. A befektetők variancia segítségével becsülik meg egy adott befektetés kockázatát.
Például egy részvény értékének egy bizonyos időszakra vonatkozó értékének kiszámításával jó képet kaphat a múltbeli volatilitásáról. Feltételezve, hogy a múlt megjósolja a jövőt, ez azt jelentené, hogy valami alacsony szórással biztonságosabb és kiszámíthatóbb.
Összehasonlíthatja valaminek a különböző időszakok eltéréseit is. Ez segíthet észlelni, ha egy másik rejtett tényező befolyásol valamit, megváltoztatja annak varianciáját.
A variancia szintén szorosan összefügg egy másik, a szórás néven ismert statisztikával. Ne feledje, hogy a variancia kiszámításához használt értékek négyzetesek. Ez azt jelenti, hogy a variancia nem az eredeti érték azonos egységében van kifejezve. A szóráshoz meg kell venni a variancia négyzetgyökét, hogy az értéket visszaállítsuk az eredeti mértékegységre. Tehát ha az adat kilogrammban volt, akkor a szórása is az.
Választás a populáció és a minta variancia között
Az Excelben a variancia két altípusa van, amelyek képletei kissé eltérőek. Az adatoktól függ, hogy melyiket válassza. Ha az adatok a teljes „populációt” tartalmazzák, akkor használjon populációs varianciát. Ebben az esetben a „populáció” azt jelenti, hogy minden értékkel rendelkezel a célcsoport minden tagja számára.

Például, ha a balkezes emberek súlyát nézzük, akkor a népességbe beletartozik minden balkezes egyed a Földön. Ha mindegyiket mérlegelte, akkor a populációs varianciát használná.
Természetesen a való életben általában megelégszünk egy kisebb mintával egy nagyobb populációból. Ebben az esetben használjon mintavarianciát. A populáció varianciája még mindig praktikus kisebb populációk esetén. Például egy vállalatnak néhány száz vagy néhány ezer alkalmazottja van, minden alkalmazottra vonatkozó adatokkal. Statisztikai értelemben vett „populációt” képviselnek.
A megfelelő szórásképlet kiválasztása
Az Excelben három minta varianciaképlet és három populációs varianciaképlet található:
- VAR , VAR.S és VARA a minta varianciájához.
- VARP , VAR.P és VARPA a populációs varianciához.
A VAR és a VARP figyelmen kívül hagyható. Ezek elavultak, és csak a régi táblázatokkal való kompatibilitás miatt érhetők el.
Marad a VAR.S és a VAR.P, amelyek egy számértékkészlet szórásának számítására szolgálnak, valamint a VARA és VARPA, amelyek szöveges karakterláncokat tartalmaznak.

A VARA és a VARPA bármely szöveges karakterláncot 0 számértékre konvertál, kivéve az „IGAZ” és „HAMIS” értéket. Ezeket a rendszer 1-re, illetve 0-ra konvertálja.
A legnagyobb különbség az, hogy a VAR.S és a VAR.P átugorja a nem numerikus értékeket. Ez kizárja azokat az eseteket az értékek teljes számából, ami azt jelenti, hogy az átlagérték eltérő lesz, mivel az átlagot kisebb számú esettel osztja el.
Hogyan számítsuk ki az eltérést az Excelben
A variancia kiszámításához az Excelben mindössze egy értékkészletre van szükség. Az alábbi példában a VAR.S-t fogjuk használni, de a képlet és a módszerek pontosan ugyanazok, függetlenül attól, hogy melyik varianciaképletet használja:
- Feltéve, hogy készen áll egy tartomány vagy diszkrét értékkészlet, válassza ki a választott üres cellát .
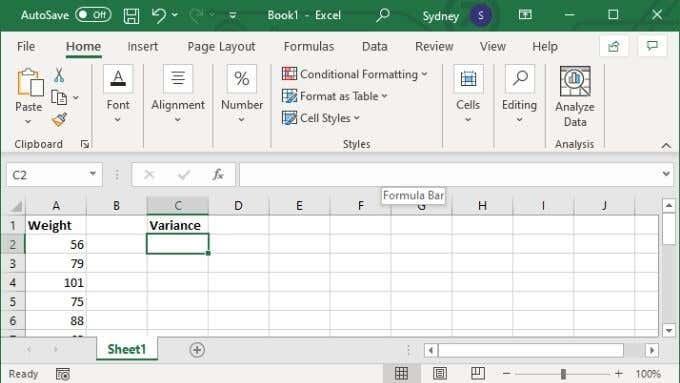
- A képletmezőbe írja be a =VAR.S(XX:YY) értéket, ahol az X és Y értékeket a tartomány első és utolsó cellaszáma váltja fel.
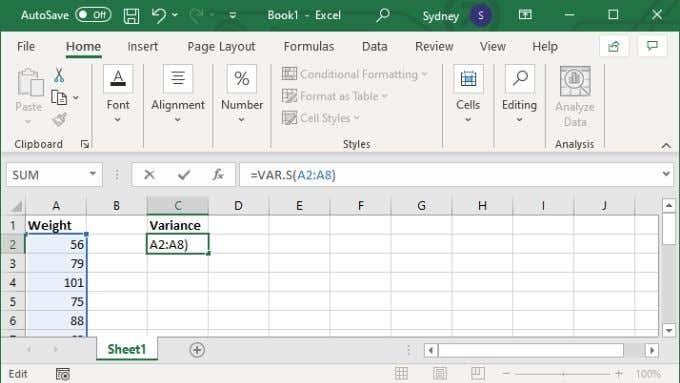
- Nyomja meg az Entert a számítás befejezéséhez.
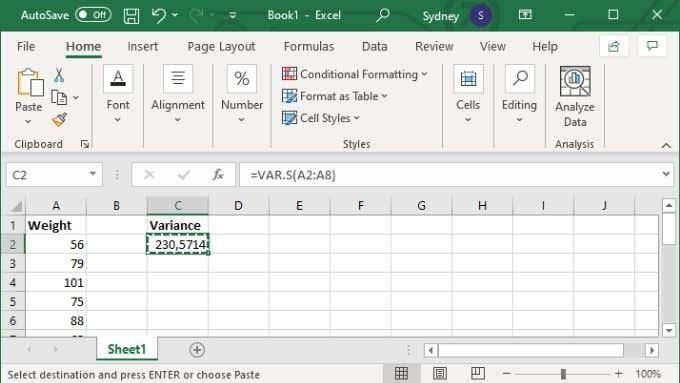
Alternatív megoldásként megadhat konkrét értékeket is, ebben az esetben a képlet így néz ki: =VAR.S(1,2,3,4) . A számokat helyettesítve azzal, amivel ki kell számítani a szórását. Legfeljebb 254 értéket adhat meg manuálisan így, de ha csak néhány értékkel rendelkezik, szinte mindig jobb, ha az adatokat egy cellatartományban adja meg, majd a fent tárgyalt képlet cellatartomány-verzióját használja.
Excelelhet itt: Er, Excel
A variancia kiszámítása hasznos trükk, amelyet mindenkinek tudnia kell, akinek statisztikai munkát kell végeznie az Excelben. Ha azonban a cikkben használt Excel terminológiák bármelyike megtévesztő volt, tekintse meg a Microsoft Excel alapismeretek oktatóanyagát – Az Excel használatának elsajátítása .
Ha viszont többre is készen áll, nézze meg a Lineáris regressziós trendvonal hozzáadása Excel-szórásdiagramhoz című részt , hogy megjelenítse a variancia vagy az adatkészlet bármely más aspektusát az aritmetikai átlaghoz képest.
Figyelmen kívül hagyható a szórás?
A variancia a valószínűségszámítás és a statisztika egyik leghasznosabb eszköze. Egy adathalmaz változékonyságának mérésére szolgál. A variancia azonban nem hagyható figyelmen kívül a statisztikában, mert segít az adatok változékonyságának értékelésében és fontos következtetések levonásában a változók közötti kapcsolatról. Ha figyelmen kívül hagyja az eltéréseket, fontos információkat hagyhat ki az adataival kapcsolatban, és félrevezető eredményekhez vezethet. Ezért a legjobb, ha nem hagyja figyelmen kívül a statisztikai eltéréseket.