Så du har blivit ombedd att beräkna varians med Excel, men du är inte säker på vad det betyder eller hur du gör det. Oroa dig inte, det är ett enkelt koncept och ännu enklare process. Du kommer att bli ett variansproffs på nolltid!
Vad är varians?
"Varians" är ett sätt att mäta medelavståndet från medelvärdet. "Medel" är summan av alla värden i en datauppsättning delat med antalet värden. Varians ger oss en uppfattning om huruvida värdena i den datamängden tenderar att i genomsnitt hålla sig enhetligt till medelvärdet eller spridas överallt.

Matematiskt är variansen inte så komplex:
- Beräkna medelvärdet av en uppsättning värden. För att beräkna medelvärdet, ta summan av alla värden delat med antalet värden.
- Ta varje värde i din uppsättning och subtrahera det från medelvärdet.
- Kvadra de resulterande värdena (för att ta bort negativa tal).
- Lägg ihop alla värden i kvadrat.
- Beräkna medelvärdet av de kvadratiska värdena för att få variansen.
Så som du kan se är det inte ett svårt värde att beräkna. Men om du har hundratals eller tusentals värden skulle det ta en evighet att göra manuellt. Så det är bra att Excel kan automatisera processen!
Vad använder du varians till?
Varians i sig har ett antal användningsområden. Ur ett rent statistiskt perspektiv är det ett bra sätt att uttrycka hur utspridda en uppsättning data är. Investerare använder varians för att uppskatta risken för en given investering.
Till exempel, genom att ta en akties värde över en tidsperiod och beräkna dess varians, får du en god uppfattning om dess volatilitet i det förflutna. Under antagandet att det förflutna förutsäger framtiden skulle det innebära att något med låg varians är säkrare och mer förutsägbart.
Du kan också jämföra varianserna för något över olika tidsperioder. Detta kan hjälpa till att upptäcka när en annan dold faktor påverkar något, ändra dess varians.
Varians är också starkt relaterad till en annan statistik som kallas standardavvikelsen. Kom ihåg att värdena som används för att beräkna variansen är kvadratiska. Detta innebär att variansen inte uttrycks i samma enhet av det ursprungliga värdet. Standardavvikelsen kräver att kvadratroten av variansen tas för att återställa värdet till dess ursprungliga enhet. Så om uppgifterna var i kilogram så är standardavvikelsen det också.
Att välja mellan population och provvarians
Det finns två undertyper av varians med lite olika formler i Excel. Vilken du ska välja beror på dina uppgifter. Om din data inkluderar hela "populationen" bör du använda populationsvarians. I det här fallet betyder "population" att du har alla värden för varje medlem av målgruppen.

Till exempel, om du tittar på vikten av vänsterhänta människor, så inkluderar befolkningen varje individ på jorden som är vänsterhänt. Om du har vägt dem alla, skulle du använda populationsvarians.
Naturligtvis nöjer vi oss i det verkliga livet med ett mindre urval från en större population. I så fall skulle du använda provvarians. Befolkningsvariation är fortfarande praktiskt med mindre populationer. Ett företag kan till exempel ha några hundra eller några tusen anställda med uppgifter om varje anställd. De representerar en "befolkning" i statistisk mening.
Att välja rätt variansformel
Det finns tre exempelvariansformler och tre populationsvariansformler i Excel:
- VAR , VAR.S och VARA för provvarians.
- VARP , VAR.P och VARPA för populationsvarians.
Du kan ignorera VAR och VARP. Dessa är föråldrade och finns bara för kompatibilitet med äldre kalkylblad.
Det lämnar VAR.S och VAR.P, som är till för att beräkna variansen för en uppsättning numeriska värden och VARA och VARPA, som inkluderar textsträngar.

VARA och VARPA kommer att konvertera vilken textsträng som helst till det numeriska värdet 0, med undantag för "TRUE" och "FALSE". Dessa konverteras till 1 respektive 0.
Den största skillnaden är att VAR.S och VAR.P hoppar över alla icke-numeriska värden. Detta exkluderar dessa fall från det totala antalet värden, vilket innebär att medelvärdet kommer att vara annorlunda, eftersom du dividerar med ett mindre antal fall för att få medelvärdet.
Hur man beräknar varians i Excel
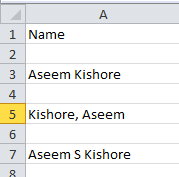
Allt du behöver för att beräkna varians i Excel är en uppsättning värden. Vi kommer att använda VAR.S i exemplet nedan, men formeln och metoderna är exakt desamma oavsett vilken variansformel du använder:
- Förutsatt att du har ett intervall eller en diskret uppsättning värden redo, välj den tomma cell du väljer.
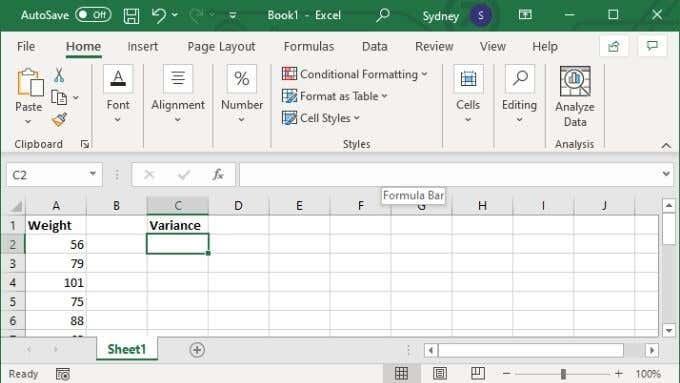
- I formelfältet skriver du =VAR.S(XX:YY) där X- och Y-värdena ersätts med de första och sista cellnumren i intervallet.
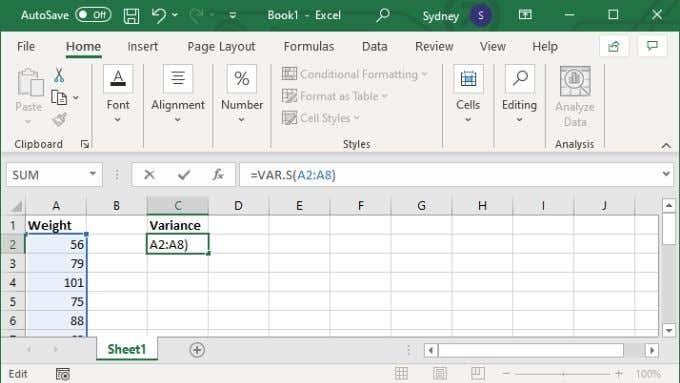
- Tryck på Enter för att slutföra beräkningen.
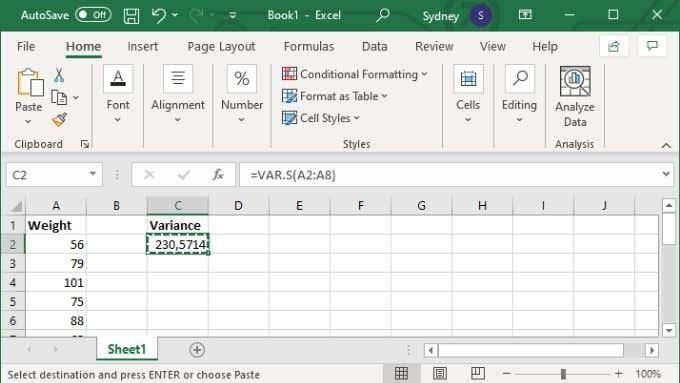
Alternativt kan du ange specifika värden, i vilket fall formeln ser ut som =VAR.S(1,2,3,4) . Med siffrorna ersatta med vad du behöver för att beräkna variansen av. Du kan ange upp till 254 värden manuellt så här, men om du inte bara har en handfull värden är det nästan alltid bättre att ange dina data i ett cellintervall och sedan använda cellintervallsversionen av formeln som diskuteras ovan.
Du kan Excel på, Eh, Excel
Att beräkna varians är ett användbart knep att veta för alla som behöver göra lite statistiskt arbete i Excel. Men om någon av Excel-terminologin vi använde i den här artikeln var förvirrande, överväg att kolla in Microsoft Excel Basics Tutorial – Lär dig hur man använder Excel .
Om du å andra sidan är redo för mer, kolla in Lägg till en linjär regressionstrendlinje till en Excel-spridningsplot så att du kan visualisera varians eller någon annan aspekt av din datamängd i förhållande till det aritmetiska medelvärdet.
Kan variansen ignoreras?
Varians är ett av de mest användbara verktygen inom sannolikhetsteori och statistik. Den används för att mäta variabiliteten hos en datamängd. Varians kan dock inte ignoreras i statistik eftersom det hjälper till att utvärdera variabiliteten av data och dra viktiga slutsatser om förhållandet mellan variabler. Om du ignorerar avvikelser kan du missa viktig information om dina data och leda till missvisande resultat. Så det är bäst att inte ignorera variansen i din statistik.