Så du er blevet bedt om at beregne varians ved hjælp af Excel, men du er ikke sikker på, hvad det betyder, eller hvordan du gør det. Bare rolig, det er et nemt koncept og endnu nemmere proces. Du bliver en varians-pro på ingen tid!
Hvad er varians?
"Varians" er en måde at måle den gennemsnitlige afstand fra middelværdien. "Middelværdien" er summen af alle værdier i et datasæt divideret med antallet af værdier. Varians giver os en idé om, hvorvidt værdierne i det pågældende datasæt har en tendens til i gennemsnit at holde sig ensartet til middelværdien eller spredes over det hele.

Matematisk er varians ikke så kompleks:
- Beregn middelværdien af et sæt værdier. For at beregne middelværdien skal du tage summen af alle værdierne divideret med antallet af værdier.
- Tag hver værdi i dit sæt og træk den fra middelværdien.
- Kvadrate de resulterende værdier (for at udligne negative tal).
- Læg alle de kvadrerede værdier sammen.
- Beregn middelværdien af de kvadrerede værdier for at få variansen.
Så som du kan se, er det ikke en svær værdi at beregne. Men hvis du har hundredvis eller tusindvis af værdier, vil det tage evigheder at gøre manuelt. Så det er en god ting, at Excel kan automatisere processen!
Hvad bruger du varians til?
Varians i sig selv har en række anvendelser. Fra et rent statistisk perspektiv er det en god forkortning til at udtrykke, hvor spredt et sæt data er. Investorer bruger varians til at estimere risikoen ved en given investering.
For eksempel, ved at tage en akties værdi over en periode og beregne dens varians, får du en god idé om dens volatilitet i fortiden. Under den antagelse, at fortiden forudsiger fremtiden, ville det betyde, at noget med lav varians er sikrere og mere forudsigeligt.
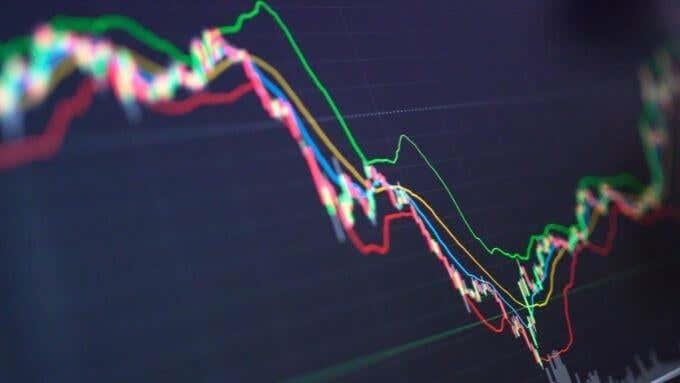
Du kan også sammenligne varianserne af noget på tværs af forskellige tidsperioder. Dette kan hjælpe med at opdage, hvornår en anden skjult faktor påvirker noget, og ændrer dets varians.
Varians er også stærkt relateret til en anden statistik kendt som standardafvigelsen. Husk, at de værdier, der bruges til at beregne varians, er i anden. Det betyder, at varians ikke er udtrykt i den samme enhed af den oprindelige værdi. Standardafvigelsen kræver, at man tager kvadratroden af variansen for at returnere værdien til dens oprindelige enhed. Så hvis dataene var i kilogram, er standardafvigelsen det også.
Valg mellem population og prøvevarians
Der er to undertyper af varians med lidt forskellige formler i Excel. Hvilken du skal vælge afhænger af dine data. Hvis dine data inkluderer hele "populationen", skal du bruge populationsvarians. I dette tilfælde betyder "befolkning", at du har enhver værdi for hvert medlem af målgruppen.

For eksempel, hvis du ser på vægten af venstrehåndede mennesker, så inkluderer befolkningen hvert individ på Jorden, der er venstrehåndet. Hvis du har vejet dem alle, ville du bruge populationsvarians.
Selvfølgelig nøjes vi i det virkelige liv med en mindre stikprøve fra en større population. I så fald ville du bruge prøvevarians. Befolkningsvarians er stadig praktisk med mindre populationer. For eksempel kan en virksomhed have nogle få hundrede eller få tusinde ansatte med data om hver medarbejder. De repræsenterer en "befolkning" i statistisk forstand.
Valg af den rigtige variansformel
Der er tre prøvevariansformler og tre populationsvariansformler i Excel:
- VAR , VAR.S og VARA for prøvevarians.
- VARP , VAR.P og VARPA for populationsvarians.
Du kan ignorere VAR og VARP. Disse er forældede og findes kun for kompatibilitet med ældre regneark.
Det efterlader VAR.S og VAR.P, som er til beregning af variansen af et sæt numeriske værdier og VARA og VARPA, som inkluderer tekststrenge.

VARA og VARPA vil konvertere enhver tekststreng til den numeriske værdi 0, med undtagelse af "TRUE" og "FALSE". Disse konverteres til henholdsvis 1 og 0.
Den største forskel er, at VAR.S og VAR.P springer over eventuelle ikke-numeriske værdier. Dette udelukker disse tilfælde fra det samlede antal værdier, hvilket betyder, at middelværdien vil være anderledes, fordi du dividerer med et mindre antal tilfælde for at få middelværdien.
Hvordan man beregner varians i Excel
Alt du behøver for at beregne varians i Excel er et sæt værdier. Vi kommer til at bruge VAR.S i eksemplet nedenfor, men formlen og metoderne er nøjagtig de samme, uanset hvilken variansformel du bruger:
- Hvis du antager, at du har et område eller et diskret sæt værdier klar, skal du vælge den tomme celle efter eget valg.
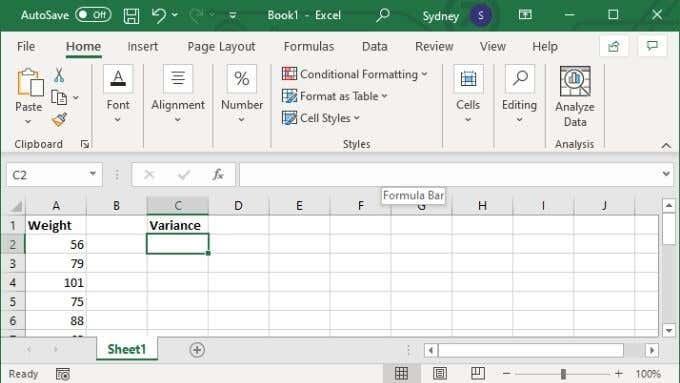
- I formelfeltet skal du skrive =VAR.S(XX:YY), hvor X- og Y-værdierne erstattes af det første og sidste cellenummer i området.
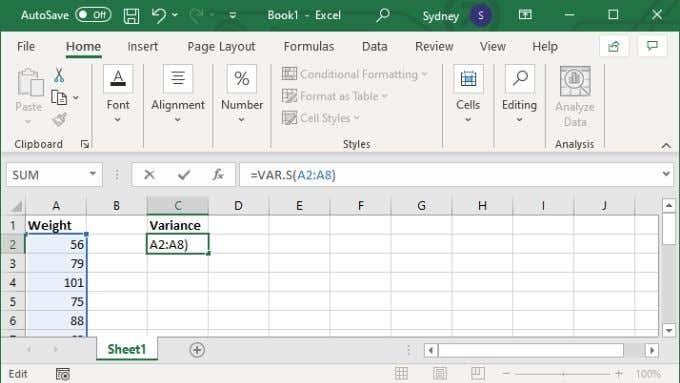
- Tryk på Enter for at fuldføre beregningen.
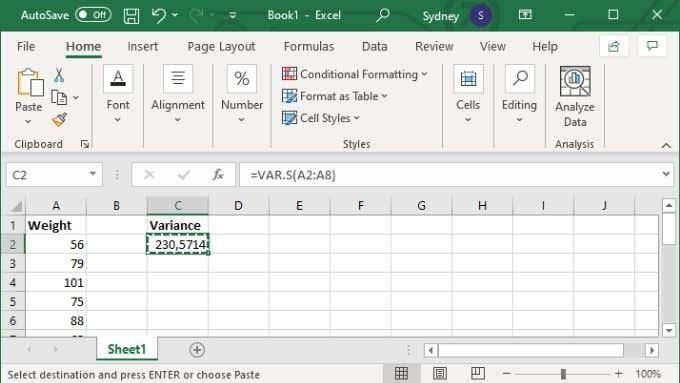
Alternativt kan du angive specifikke værdier, i hvilket tilfælde formlen ser ud som =VAR.S(1,2,3,4) . Med tallene erstattet med det, du skal bruge for at beregne variansen af. Du kan indtaste op til 254 værdier manuelt på denne måde, men medmindre du kun har en håndfuld værdier, er det næsten altid bedre at indtaste dine data i et celleområde og derefter bruge celleområdeversionen af formlen diskuteret ovenfor.
Du kan Excel på, Eh, Excel
Beregning af varians er et nyttigt trick for alle, der har brug for at udføre noget statistisk arbejde i Excel. Men hvis nogen af de Excel-terminologier, vi brugte i denne artikel, var forvirrende, kan du overveje at tjekke Microsoft Excel Basics Tutorial – Lær at bruge Excel .
Hvis du på den anden side er klar til mere, så tjek Tilføj en lineær regressionstendenslinje til et Excel -spredningsplot , så du kan visualisere varians eller ethvert andet aspekt af dit datasæt i forhold til det aritmetiske gennemsnit.
Kan varians ignoreres?
Varians er et af de mest nyttige værktøjer inden for sandsynlighedsteori og statistik. Det bruges til at måle variabiliteten af et datasæt. Varians kan dog ikke ignoreres i statistik, fordi det hjælper med at evaluere variabiliteten af data og drage vigtige konklusioner om forholdet mellem variabler. Hvis du ignorerer afvigelser, kan du gå glip af vigtige oplysninger om dine data og føre til vildledende resultater. Så det er bedst ikke at ignorere varians i dine statistikker.