Svo þú hefur verið beðinn um að reikna dreifni með Excel, en þú ert ekki viss um hvað það þýðir eða hvernig á að gera það. Ekki hafa áhyggjur, þetta er auðvelt hugtak og jafnvel auðveldara ferli. Þú verður afbrigði atvinnumaður á skömmum tíma!
Hvað er afbrigði?
„Frávik“ er leið til að mæla meðalfjarlægð frá meðaltali. „Meðaltalið“ er summa allra gilda í gagnasafni deilt með fjölda gilda. Frávik gefur okkur hugmynd um hvort gildin í því gagnasafni hafa tilhneigingu að meðaltali til að haldast jafnt við meðaltalið eða dreifast út um allt.

Stærðfræðilega er dreifni ekki svo flókin:
- Reiknaðu meðaltal gildismengis. Til að reikna meðaltalið skaltu taka summu allra gilda deilt með fjölda gilda.
- Taktu hvert gildi í settinu þínu og dragðu það frá meðaltalinu.
- Kvaðrataðu gildin sem myndast (til að hætta við neikvæðar tölur).
- Leggðu öll gildin í veldi saman.
- Reiknið meðaltal í öðru veldi til að fá dreifni.
Svo eins og þú sérð er það ekki erfitt að reikna það út. Hins vegar, ef þú ert með hundruð eða þúsundir gilda, myndi það taka eilífð að gera það handvirkt. Svo það er gott að Excel geti gert ferlið sjálfvirkt!
Í hvað notarðu Variance?
Frávik í sjálfu sér hefur margvíslega notkun. Frá eingöngu tölfræðilegu sjónarhorni er það góð stuttmynd til að tjá hversu dreifð gagnasafnið er. Fjárfestar nota dreifni til að meta áhættu tiltekinnar fjárfestingar.
Til dæmis, með því að taka verðmæti hlutabréfa yfir ákveðið tímabil og reikna út dreifni þess, færðu góða hugmynd um sveiflur í fortíðinni. Með þeirri forsendu að fortíðin spái fyrir um framtíðina myndi það þýða að eitthvað með litla dreifni sé öruggara og fyrirsjáanlegra.
Þú getur líka borið saman frávik einhvers á mismunandi tímabilum. Þetta getur hjálpað til við að greina hvenær annar falinn þáttur hefur áhrif á eitthvað, breytir fráviki þess.
Frávik er einnig sterklega tengt annarri tölfræði sem kallast staðalfrávik. Mundu að gildin sem notuð eru til að reikna dreifni eru í öðru veldi. Þetta þýðir að dreifni er ekki gefin upp í sömu einingu upprunalega gildisins. Staðalfrávikið krefst þess að kvaðratrót dreifni sé tekin til að skila gildinu í upprunalegu eininguna. Þannig að ef gögnin voru í kílóum þá er staðalfrávikið líka.
Velja á milli íbúafjölda og sýnishornafbrigðis
Það eru tvær undirgerðir af dreifni með aðeins mismunandi formúlum í Excel. Hver þú ættir að velja fer eftir gögnum þínum. Ef gögnin þín innihalda allan „íbúafjöldann“ þá ættir þú að nota þýðisfrávik. Í þessu tilviki þýðir „íbúafjöldi“ að þú hafir öll gildi fyrir hvern meðlim markhópsins.

Til dæmis, ef þú ert að skoða þyngd örvhents fólks, þá inniheldur íbúafjöldinn hvern einstakling á jörðinni sem er örvhentur. Ef þú hefur vegið þá alla, myndir þú nota þýðisfrávik.
Auðvitað, í raunveruleikanum sættum við okkur venjulega við minna úrtak úr stærri þýði. Í því tilviki myndir þú nota sýnishornafbrigði. Mannfjöldafrávik er enn hagkvæmt með minni íbúa. Til dæmis getur fyrirtæki haft nokkur hundruð eða nokkur þúsund starfsmenn með gögn um hvern starfsmann. Þeir tákna „íbúafjölda“ í tölfræðilegum skilningi.
Að velja réttu afbrigðisformúluna
Það eru þrjár sýnisfráviksformúlur og þrjár þýðisfráviksformúlur í Excel:
- VAR , VAR.S og VARA fyrir úrtaksfrávik.
- VARP , VAR.P og VARPA fyrir íbúafrávik.
Þú getur hunsað VAR og VARP. Þetta eru gamaldags og eru aðeins til vegna samhæfni við eldri töflureikna.
Það skilur eftir VAR.S og VAR.P, sem eru til að reikna út dreifni safns tölugilda og VARA og VARPA, sem innihalda textastrengi.

VARA og VARPA munu breyta hvaða textastreng sem er í tölugildið 0, að undanskildum „TRUE“ og „FALSE“. Þessum er breytt í 1 og 0 í sömu röð.
Stærsti munurinn er sá að VAR.S og VAR.P sleppa öllum ótölugildum. Þetta útilokar þessi tilvik frá heildarfjölda gilda, sem þýðir að meðalgildið verður öðruvísi, vegna þess að þú ert að deila með færri tilvikum til að fá meðaltalið.
Hvernig á að reikna frávik í Excel
Allt sem þú þarft til að reikna dreifni í Excel er sett af gildum. Við ætlum að nota VAR.S í dæminu hér að neðan, en formúlan og aðferðirnar eru nákvæmlega eins óháð því hvaða dreifniformúla þú notar:
- Að því gefnu að þú hafir svið eða stakt gildissett tilbúið skaltu velja tóma reitinn að eigin vali.
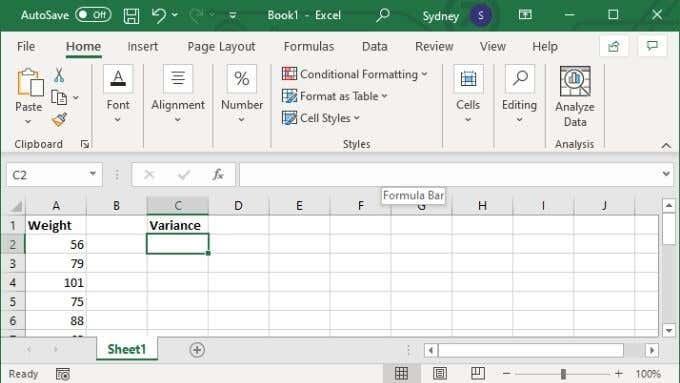
- Í formúlareitnum, sláðu inn =VAR.S(XX:YY) þar sem X og Y gildin eru skipt út fyrir fyrsta og síðasta reit númer sviðsins.
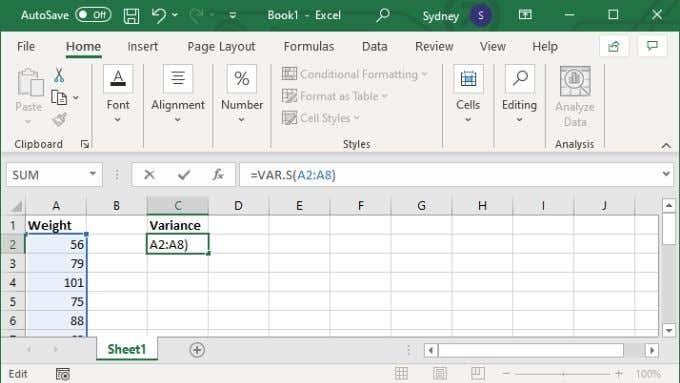
- Ýttu á Enter til að klára útreikninginn.
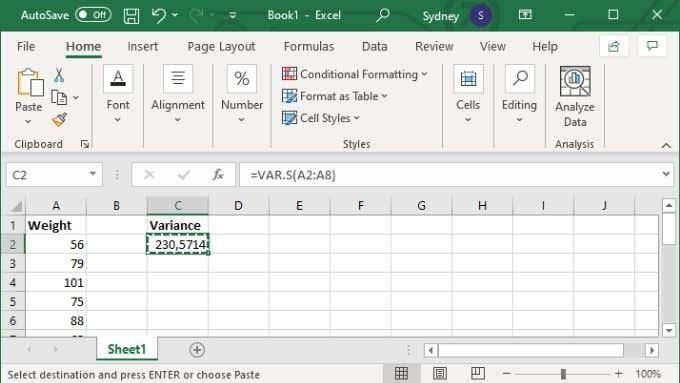
Að öðrum kosti geturðu tilgreint ákveðin gildi, en þá lítur formúlan út eins og =VAR.S(1,2,3,4) . Með tölunum skipt út fyrir það sem þú þarft til að reikna út dreifni. Þú getur slegið inn allt að 254 gildi handvirkt eins og þetta, en nema þú hafir aðeins handfylli af gildum er næstum alltaf betra að slá inn gögnin þín í reitsvið og nota síðan frumusviðsútgáfu formúlunnar sem fjallað er um hér að ofan.
Þú getur Excel á, Er, Excel
Að reikna dreifni er gagnlegt bragð til að vita fyrir alla sem þurfa að vinna tölfræðivinnu í Excel. En ef eitthvað af Excel hugtökum sem við notuðum í þessari grein var ruglingslegt skaltu íhuga að skoða Microsoft Excel Basics Tutorial - Lærðu hvernig á að nota Excel .
Ef þú ert aftur á móti tilbúinn í meira, skoðaðu Bæta línulegri aðhvarfslínu við Excel dreifingarmynd svo þú getir séð frávik eða annan þátt gagnasettsins í tengslum við reiknað meðaltal.
Er hægt að hunsa frávik?
Dreifni er eitt af gagnlegustu verkfærunum í líkindafræði og tölfræði. Það er notað til að mæla breytileika gagnasafns. Hins vegar er ekki hægt að hunsa frávik í tölfræði vegna þess að það hjálpar til við að meta breytileika gagna og draga mikilvægar ályktanir um tengsl milli breyta. Ef þú hunsar frávik gætirðu misst mikilvægar upplýsingar um gögnin þín og leitt til villandi niðurstaðna. Svo það er best að hunsa ekki frávik í tölfræðinni þinni.