Per tant, se us ha demanat que calculeu la variància mitjançant Excel, però no esteu segur de què significa això ni de com fer-ho. No us preocupeu, és un concepte fàcil i un procés encara més fàcil. Seràs un professional de la variació en molt poc temps!
Què és la variància?
"Variància" és una manera de mesurar la distància mitjana de la mitjana. La "mitjana" és la suma de tots els valors d'un conjunt de dades dividida pel nombre de valors. La variància ens dóna una idea de si els valors d'aquest conjunt de dades tendeixen, de mitjana, a quedar-se uniformement a la mitjana o a dispersar-se per tot arreu.

Matemàticament, la variància no és tan complexa:
- Calcula la mitjana d'un conjunt de valors. Per calcular la mitjana, pren la suma de tots els valors dividit pel nombre de valors.
- Preneu tots els valors del vostre conjunt i resteu-los de la mitjana.
- Quadrat els valors resultants (per cancel·lar nombres negatius).
- Sumeu tots els valors al quadrat.
- Calcula la mitjana dels valors quadrats per obtenir la variància.
Així, com podeu veure, no és un valor difícil de calcular. Tanmateix, si teniu centenars o milers de valors, trigaria una eternitat a fer-ho manualment. Per tant, és bo que Excel pugui automatitzar el procés!
Per a què utilitzeu la variància?
La variació per si mateixa té diversos usos. Des d'una perspectiva purament estadística, és una bona manera taquigràfica d'expressar la distribució d'un conjunt de dades. Els inversors utilitzen la variància per estimar el risc d'una inversió determinada.
Per exemple, prenent el valor d' una acció durant un període de temps i calculant la seva variància, tindreu una bona idea de la seva volatilitat en el passat. Sota l'assumpció que el passat prediu el futur, significaria que alguna cosa amb poca variància és més segura i més previsible.
També podeu comparar les variacions d'alguna cosa en diferents períodes de temps. Això pot ajudar a detectar quan un altre factor ocult està influint en alguna cosa, canviant-ne la variància.
La variància també està fortament relacionada amb una altra estadística coneguda com a desviació estàndard. Recordeu que els valors utilitzats per calcular la variància són al quadrat. Això vol dir que la variància no s'expressa en la mateixa unitat del valor original. La desviació estàndard requereix prendre l'arrel quadrada de la variància per tornar el valor a la seva unitat original. Per tant, si les dades estaven en quilograms, la desviació estàndard també ho és.
Escollir entre la població i la variància mostral
Hi ha dos subtipus de variància amb fórmules lleugerament diferents a Excel. Quin hauríeu de triar depèn de les vostres dades. Si les vostres dades inclouen tota la "població", hauríeu d'utilitzar la variància de la població. En aquest cas, "població" significa que teniu tots els valors per a cada membre del grup de població objectiu.

Per exemple, si observeu el pes de les persones esquerranes, aleshores la població inclou tots els individus de la Terra que són esquerrans. Si els heu pesat tots, utilitzareu la variància de la població.
Per descomptat, a la vida real normalment ens conformem amb una mostra més petita d'una població més gran. En aquest cas, utilitzaràs la variància de mostra. La variació de la població encara és pràctica amb poblacions més petites. Per exemple, una empresa pot tenir uns quants centenars o pocs milers d'empleats amb dades de cada empleat. Representen una "població" en el sentit estadístic.
Selecció de la fórmula de variància correcta
Hi ha tres fórmules de variància de mostra i tres fórmules de variància poblacional a Excel:
- VAR , VAR.S i VARA per a la variància mostral.
- VARP , VAR.P i VARPA per a la variància poblacional.
Podeu ignorar el VAR i el VARP. Aquests estan obsolets i només estan disponibles per compatibilitat amb fulls de càlcul heretats.
Queden VAR.S i VAR.P, que serveixen per calcular la variància d'un conjunt de valors numèrics, i VARA i VARPA, que inclouen cadenes de text.

VARA i VARPA convertiran qualsevol cadena de text al valor numèric 0, amb l'excepció de "VERTADER" i "FALSE". Aquests es converteixen en 1 i 0 respectivament.
La diferència més gran és que VAR.S i VAR.P es salten qualsevol valor no numèric. Això exclou aquests casos del nombre total de valors, la qual cosa significa que el valor mitjà serà diferent, perquè esteu dividint per un nombre més petit de casos per obtenir la mitjana.
Com calcular la variància a Excel
Tot el que necessiteu per calcular la variància a Excel és un conjunt de valors. Utilitzarem VAR.S a l'exemple següent, però la fórmula i els mètodes són exactament els mateixos, independentment de quina fórmula de variància utilitzeu:
- Suposant que teniu un rang o un conjunt discret de valors a punt, seleccioneu la cel·la buida que trieu.
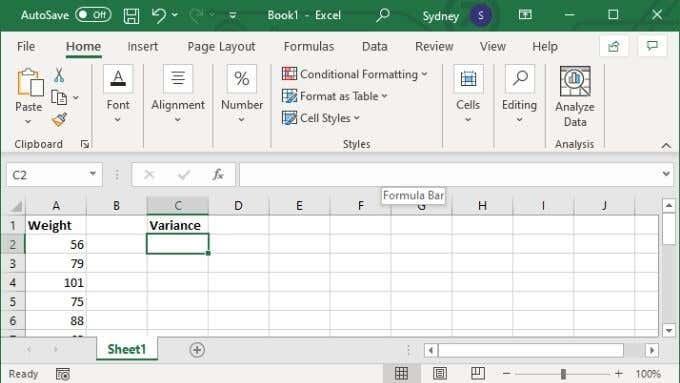
- Al camp de la fórmula, escriviu =VAR.S(XX:YY) on els valors X i Y es substitueixen pel primer i l'últim número de cel·la de l'interval.
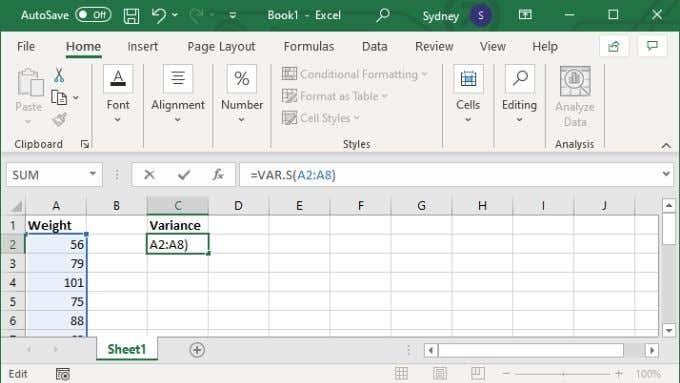
- Premeu Intro per completar el càlcul.
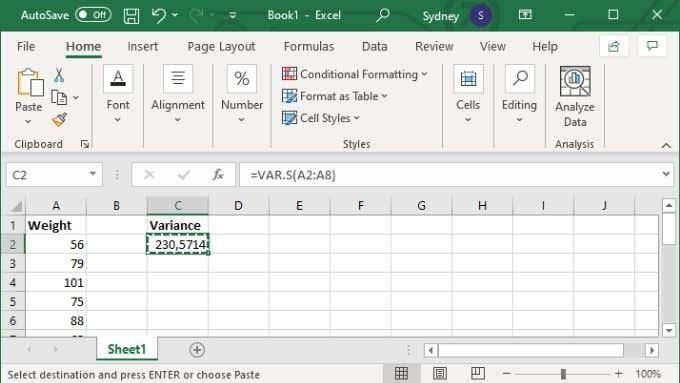
Alternativament, podeu especificar valors específics, en aquest cas la fórmula sembla =VAR.S(1,2,3,4) . Amb els números substituïts per el que necessiteu per calcular la variància. Podeu introduir fins a 254 valors manualment com aquest, però tret que només tingueu un grapat de valors, gairebé sempre és millor introduir les vostres dades en un interval de cel·les i després utilitzar la versió de l'interval de cel·les de la fórmula esmentada anteriorment.
Podeu Excel a, Er, Excel
El càlcul de la variància és un truc útil per a qualsevol persona que necessiti fer un treball estadístic a Excel. Però si alguna de la terminologia d'Excel que hem utilitzat en aquest article era confusa, penseu a consultar el tutorial bàsic de Microsoft Excel: aprendre a utilitzar Excel .
Si, d'altra banda, esteu preparat per a més, consulteu Afegeix una línia de tendència de regressió lineal a un diagrama de dispersió d'Excel perquè pugueu visualitzar la variància o qualsevol altre aspecte del vostre conjunt de dades en relació amb la mitjana aritmètica.
Es pot ignorar la variància?
La variància és una de les eines més útils en teoria i estadística de probabilitats. S'utilitza per mesurar la variabilitat d'un conjunt de dades. Tanmateix, la variància no es pot ignorar en les estadístiques perquè ajuda a avaluar la variabilitat de les dades i a treure conclusions importants sobre la relació entre variables. Si ignoreu la variació, podeu perdre informació important sobre les vostres dades i donar lloc a resultats enganyosos. Per tant, és millor no ignorar la variació de les vostres estadístiques.