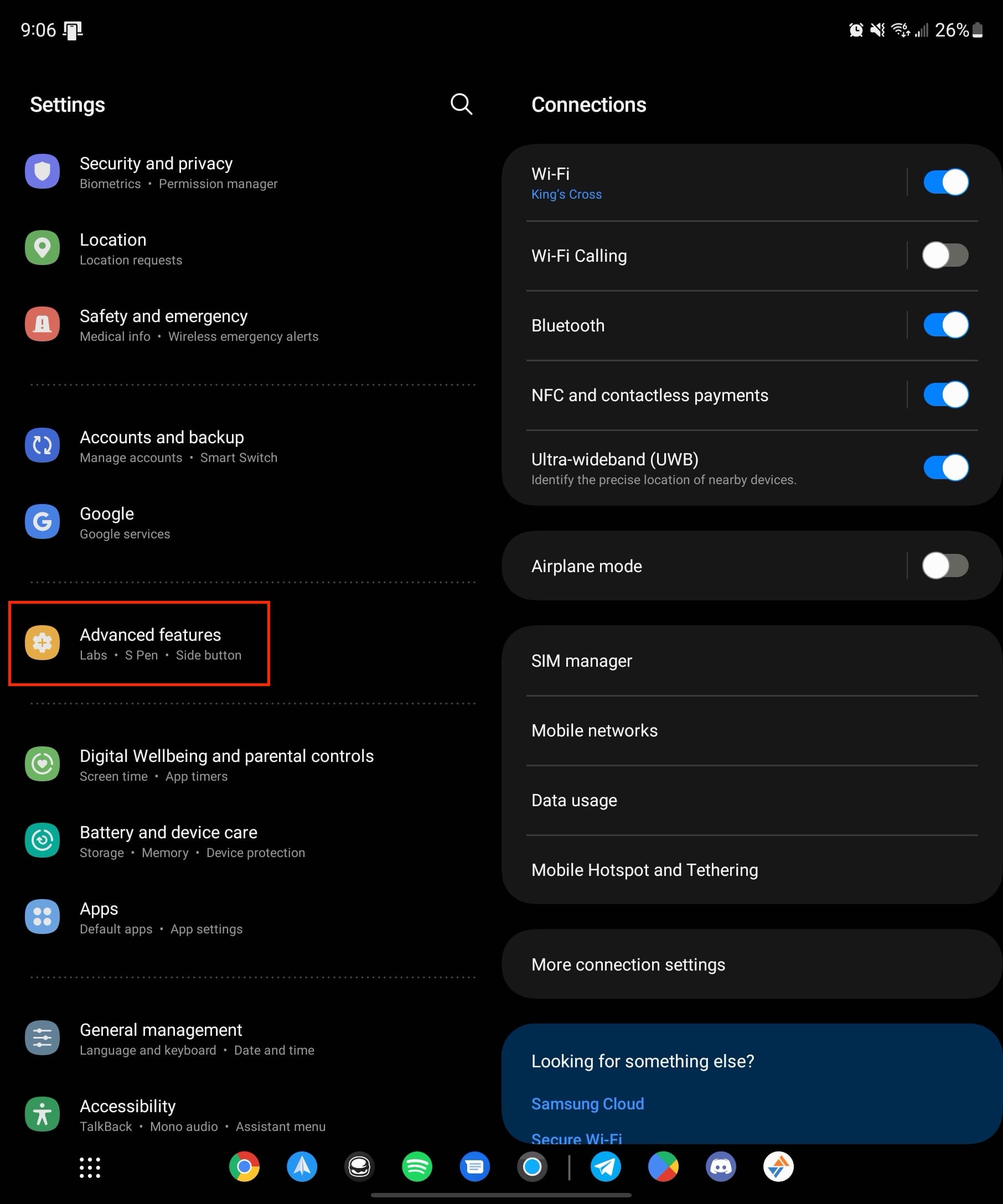
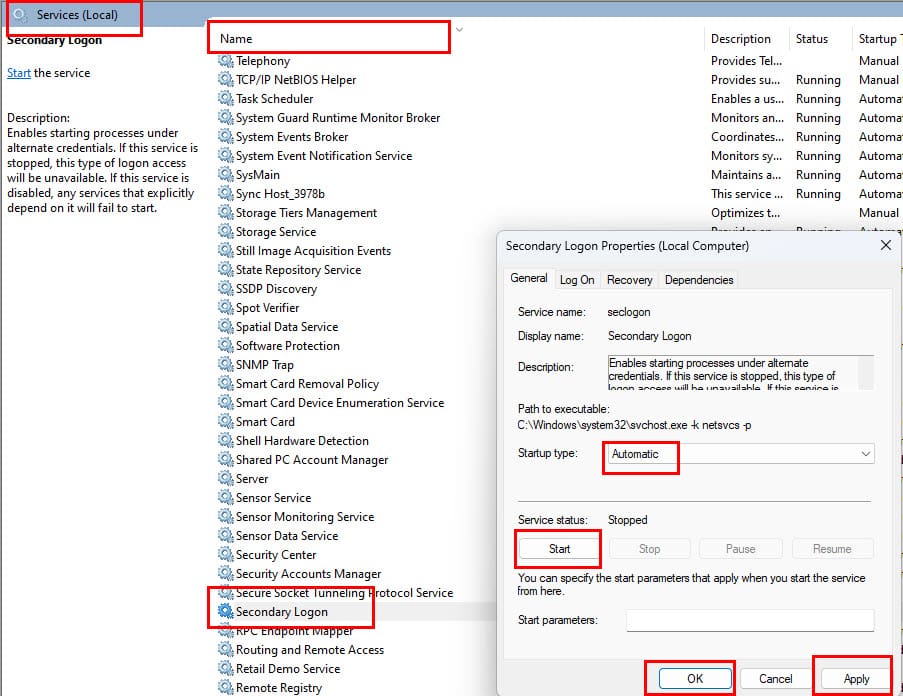
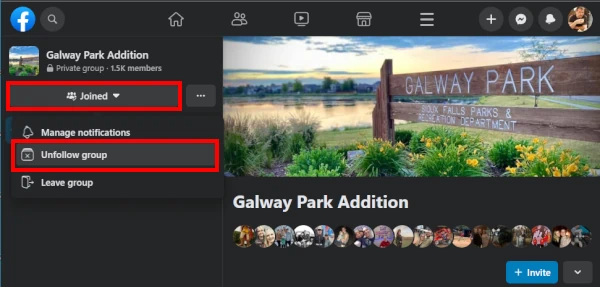
Så du har blitt bedt om å beregne varians ved hjelp av Excel, men du er ikke sikker på hva det betyr eller hvordan du gjør det. Ikke bekymre deg, det er et enkelt konsept og enda enklere prosess. Du vil bli en variansproff på kort tid!
Hva er varians?
"Varians" er en måte å måle gjennomsnittlig avstand fra gjennomsnittet. "Mean" er summen av alle verdier i et datasett delt på antall verdier. Varians gir oss en ide om hvorvidt verdiene i det datasettet har en tendens til i gjennomsnitt å holde seg jevnt til gjennomsnittet eller spre seg over alt.

Matematisk er variansen ikke så kompleks:
- Beregn gjennomsnittet av et sett med verdier. For å beregne gjennomsnittet, ta summen av alle verdiene delt på antall verdier.
- Ta hver verdi i settet ditt og trekk det fra gjennomsnittet.
- Kvaddra de resulterende verdiene (for å oppheve negative tall).
- Legg sammen alle de kvadratiske verdiene.
- Beregn gjennomsnittet av de kvadrerte verdiene for å få variansen.
Så som du kan se, er det ikke en vanskelig verdi å beregne. Men hvis du har hundrevis eller tusenvis av verdier, vil det ta evigheter å gjøre manuelt. Så det er bra at Excel kan automatisere prosessen!
Hva bruker du varians til?
Varians i seg selv har en rekke bruksområder. Fra et rent statistisk perspektiv er det en god kortfattet måte å uttrykke hvor spredt et sett med data er. Investorer bruker varians for å estimere risikoen for en gitt investering.
For eksempel, ved å ta en aksjes verdi over en periode og beregne variansen, vil du få en god ide om dens volatilitet i fortiden. Under antakelsen om at fortiden forutsier fremtiden, vil det bety at noe med lav varians er tryggere og mer forutsigbart.
Du kan også sammenligne variansene til noe på tvers av ulike tidsperioder. Dette kan bidra til å oppdage når en annen skjult faktor påvirker noe, og endrer variansen.
Varians er også sterkt relatert til en annen statistikk kjent som standardavviket. Husk at verdiene som brukes til å beregne variansen er i andre. Dette betyr at variansen ikke uttrykkes i samme enhet av den opprinnelige verdien. Standardavviket krever å ta kvadratroten av variansen for å returnere verdien til den opprinnelige enheten. Så hvis dataene var i kilo, er standardavviket det også.
Velge mellom populasjon og utvalgsvarians
Det er to undertyper av varians med litt forskjellige formler i Excel. Hvilken du bør velge avhenger av dataene dine. Hvis dataene dine inkluderer hele "populasjonen", bør du bruke populasjonsvarians. I dette tilfellet betyr "populasjon" at du har hver verdi for hvert medlem av målgruppen.

For eksempel, hvis du ser på vekten av venstrehendte mennesker, inkluderer befolkningen alle individer på jorden som er venstrehendte. Hvis du har veid dem alle, ville du brukt populasjonsvarians.
Selvfølgelig nøyer vi oss i det virkelige liv med et mindre utvalg fra en større populasjon. I så fall vil du bruke prøvevarians. Befolkningsvariasjon er fortsatt praktisk med mindre populasjoner. For eksempel kan en bedrift ha noen hundre eller få tusen ansatte med data om hver ansatt. De representerer en "befolkning" i statistisk forstand.
Velge riktig variansformel
Det er tre eksempler på variansformler og tre populasjonsvariansformler i Excel:
- VAR , VAR.S og VARA for prøvevarians.
- VARP , VAR.P og VARPA for populasjonsvarians.
Du kan ignorere VAR og VARP. Disse er utdaterte og finnes kun for kompatibilitet med eldre regneark.
Det forlater VAR.S og VAR.P, som er for å beregne variansen til et sett med numeriske verdier og VARA og VARPA, som inkluderer tekststrenger.

VARA og VARPA vil konvertere enhver tekststreng til den numeriske verdien 0, med unntak av "TRUE" og "FALSE". Disse konverteres til henholdsvis 1 og 0.
Den største forskjellen er at VAR.S og VAR.P hopper over alle ikke-numeriske verdier. Dette ekskluderer disse tilfellene fra det totale antallet verdier, noe som betyr at gjennomsnittsverdien vil være annerledes, fordi du deler med et mindre antall tilfeller for å få gjennomsnittet.
Hvordan beregne varians i Excel
Alt du trenger for å beregne varians i Excel er et sett med verdier. Vi skal bruke VAR.S i eksemplet nedenfor, men formelen og metodene er nøyaktig de samme uavhengig av hvilken variansformel du bruker:
- Forutsatt at du har et område eller et diskret sett med verdier klar, velg den tomme cellen du ønsker.
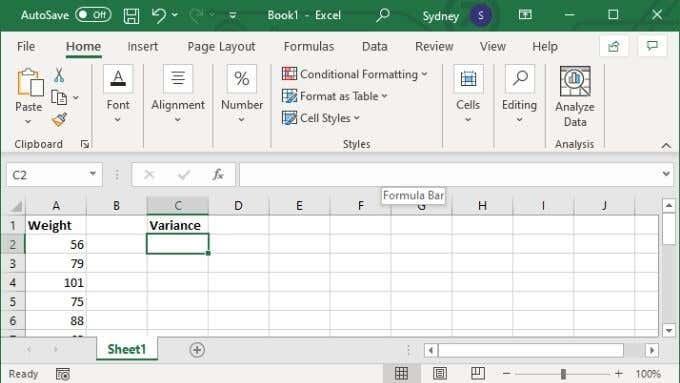
- I formelfeltet skriver du =VAR.S(XX:YY) der X- og Y-verdiene erstattes av det første og siste cellenummeret i området.
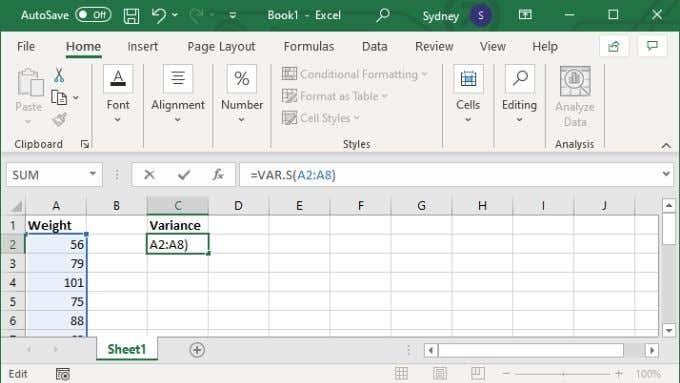
- Trykk Enter for å fullføre beregningen.
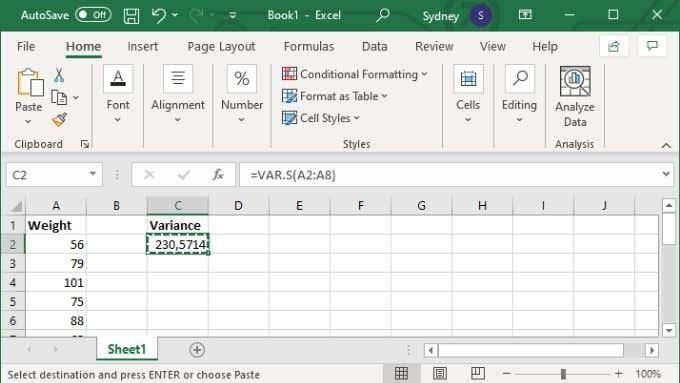
Alternativt kan du angi spesifikke verdier, i så fall ser formelen ut som =VAR.S(1,2,3,4) . Med tallene erstattet med det du trenger for å beregne variansen. Du kan legge inn opptil 254 verdier manuelt slik, men med mindre du bare har en håndfull verdier, er det nesten alltid bedre å legge inn dataene dine i et celleområde og deretter bruke celleområdeversjonen av formelen diskutert ovenfor.
Du kan Excel på, Er, Excel
Å beregne varians er et nyttig triks for alle som trenger å gjøre litt statistisk arbeid i Excel. Men hvis noen av Excel-terminologien vi brukte i denne artikkelen var forvirrende, bør du vurdere å sjekke ut Microsoft Excel Basics Tutorial – Lær hvordan du bruker Excel .
Hvis du derimot er klar for mer, sjekk Legg til en lineær regresjonstrendlinje til et Excel-spredningsplot slik at du kan visualisere varians eller andre aspekter av datasettet ditt i forhold til det aritmetiske gjennomsnittet.
Kan avvik ignoreres?
Varians er et av de mest nyttige verktøyene innen sannsynlighetsteori og statistikk. Den brukes til å måle variabiliteten til et datasett. Imidlertid kan varians ikke ignoreres i statistikk fordi det hjelper til med å evaluere variasjonen til data og trekke viktige konklusjoner om forholdet mellom variabler. Hvis du ignorerer avvik, kan du gå glipp av viktig informasjon om dataene dine og føre til misvisende resultater. Så det er best å ikke ignorere variasjoner i statistikken.