Дакле, од вас је затражено да израчунате варијансу користећи Екцел, али нисте сигурни шта то значи или како да то урадите. Не брините, то је лак концепт и још лакши процес. За кратко време ћете постати професионалац за варијансе!
Шта је варијанса?
„Варијанца“ је начин мерења просечне удаљености од средње вредности. „Просечна вредност“ је збир свих вредности у скупу података подељен бројем вредности. Варијанца нам даје представу о томе да ли вредности у том скупу података имају тенденцију, у просеку, да се уједначено држе средње вредности или се раштркају по целом месту.

Математички гледано, варијанса није тако сложена:
- Израчунајте средњу вредност скупа вредности. Да бисте израчунали средњу вредност, узмите збир свих вредности подељен бројем вредности.
- Узмите сваку вредност у свом скупу и одузмите је од средње вредности.
- Добијене вредности у квадратуру (да бисте поништили негативне бројеве).
- Додајте све вредности на квадрат.
- Израчунајте средњу вредност квадрата вредности да бисте добили варијансу.
Као што видите, није тешко израчунати вредност. Међутим, ако имате стотине или хиљаде вредности, ручно би то потрајало. Дакле, добро је што Екцел може аутоматизовати процес!
За шта користите варијансу?
Варијанца сама по себи има бројне употребе. Из чисто статистичке перспективе, то је добар скраћени начин да се изрази колико је скуп података раширен. Инвеститори користе варијансу да би проценили ризик дате инвестиције.
На пример, ако узмете вредност акције током одређеног временског периода и израчунате њену варијансу, добићете добру представу о њеној волатилности у прошлости. Под претпоставком да прошлост предвиђа будућност, то би значило да је нешто са малом варијансом сигурније и предвидљивије.
Такође можете да упоредите варијације нечега у различитим временским периодима. Ово може помоћи да се открије када други скривени фактор утиче на нешто, мењајући његову варијансу.
Варијанца је такође снажно повезана са другом статистиком познатом као стандардна девијација. Запамтите да су вредности које се користе за израчунавање варијансе стављене на квадрат. То значи да варијанса није изражена у истој јединици првобитне вредности. Стандардна девијација захтева узимање квадратног корена варијансе да би се вредност вратила на првобитну јединицу. Дакле, ако су подаци у килограмима онда је и стандардна девијација.
Избор између популације и варијансе узорка
Постоје два подтипа варијансе са мало другачијим формулама у Екцел-у. Коју ћете изабрати зависи од ваших података. Ако ваши подаци укључују целокупну „популацију“, онда би требало да користите варијансу становништва. У овом случају „популација“ значи да имате сваку вредност за сваког члана циљне групе становништва.

На пример, ако гледате тежину леворуких људи, онда популација укључује сваког појединца на Земљи који је леворуки. Ако сте их све измерили, користили бисте варијацију популације.
Наравно, у стварном животу обично се задовољавамо мањим узорком из веће популације. У том случају бисте користили узорак варијансе. Варијанца становништва је и даље практична са мањим популацијама. На пример, компанија може имати неколико стотина или неколико хиљада запослених са подацима о сваком запосленом. Они представљају „популацију“ у статистичком смислу.
Избор праве формуле варијансе
У Екцел-у постоје три формуле варијансе узорка и три формуле варијансе популације:
- ВАР , ВАР.С и ВАРА за варијансу узорка.
- ВАРП , ВАР.П и ВАРПА за варијансу популације.
Можете занемарити ВАР и ВАРП. Оне су застареле и постоје само због компатибилности са застарелим табелама.
То оставља ВАР.С и ВАР.П, који служе за израчунавање варијансе скупа нумеричких вредности и ВАРА и ВАРПА, који укључују текстуалне низове.

ВАРА и ВАРПА ће конвертовати било који текстуални низ у нумеричку вредност 0, са изузетком „ТРУЕ“ и „ФАЛСЕ“. Они се конвертују у 1 и 0 респективно.
Највећа разлика је у томе што ВАР.С и ВАР.П прескачу све ненумеричке вредности. Ово искључује те случајеве из укупног броја вредности, што значи да ће средња вредност бити другачија, јер делите са мањим бројем случајева да бисте добили средњу вредност.
Како израчунати варијансу у Екцелу
Све што вам треба да израчунате варијансу у Екцел-у је скуп вредности. Користићемо ВАР.С у примеру испод, али формула и методе су потпуно исте без обзира коју формулу варијансе користите:
- Под претпоставком да имате спреман опсег или дискретни скуп вредности, изаберите празну ћелију по свом избору.
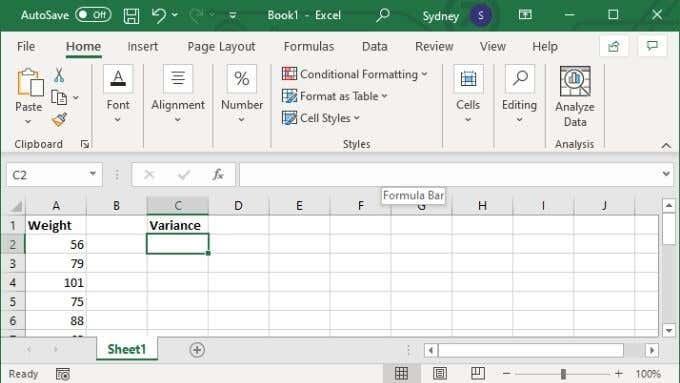
- У поље формуле откуцајте =ВАР.С(КСКС:ИИ) где су вредности Кс и И замењене првим и последњим бројем ћелије у опсегу.
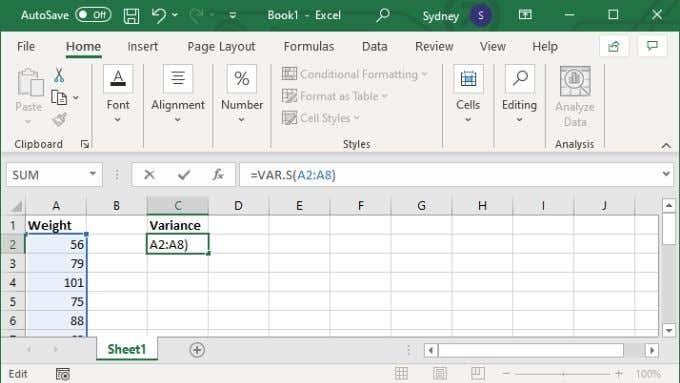
- Притисните Ентер да завршите прорачун.
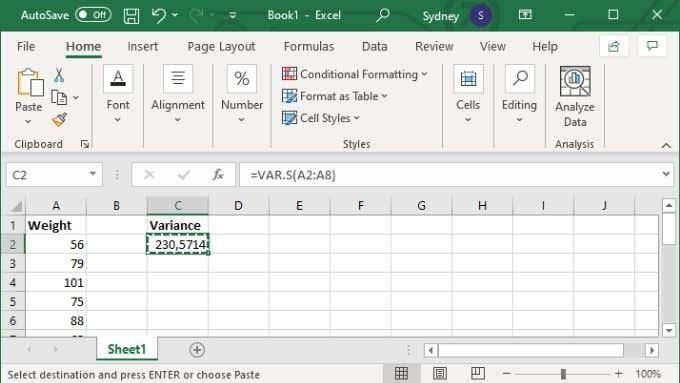
Алтернативно, можете навести одређене вредности, у ком случају формула изгледа као =ВАР.С(1,2,3,4) . Са бројевима замењеним оним што вам је потребно за израчунавање варијансе. Можете да унесете до 254 вредности ручно, као што је овај, али осим ако немате само неколико вредности, скоро увек је боље да унесете своје податке у опсег ћелија, а затим да користите верзију опсега ћелија формуле о којој смо горе говорили.
Можете Екцел у, Ер, Екцел
Израчунавање варијансе је користан трик за свакога ко треба да обави неке статистичке послове у Екцел-у. Али ако је било која од терминологије програма Екцел коју смо користили у овом чланку била збуњујућа, размислите о томе да погледате Водич за основе Мицрософт Екцел-а – Учење како да користите Екцел .
Ако сте, с друге стране, спремни за више, погледајте Додај линију тренда линеарне регресије у Екцел дијаграм распршивања како бисте могли да визуелизујете варијансу или било који други аспект вашег скупа података у односу на аритметичку средину.