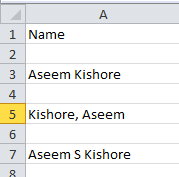
Kaip atskirti vardus ir pavardes „Excel“.
Sužinokite, kaip lengvai atskirti vardus ir pavardes „Excel“ naudojant paprastas formules arba „Tekstas į stulpelius“ funkciją.
Kaip apskaičiuoti dispersiją „Excel“.
Taigi jūsų buvo paprašyta apskaičiuoti dispersiją naudojant „Excel“, bet nesate tikri, ką tai reiškia ir kaip tai padaryti. Nesijaudinkite, tai paprasta koncepcija ir dar paprastesnis procesas. Greitai būsite variacijos profesionalas!
Kas yra dispersija?
„Variantas“ yra būdas išmatuoti vidutinį atstumą nuo vidurkio. „Vidurkis“ yra visų duomenų rinkinio verčių suma, padalyta iš reikšmių skaičiaus. Variantas leidžia suprasti, ar to duomenų rinkinio reikšmės vidutiniškai vienodai prilimpa prie vidurkio, ar išsisklaido po visą vietą.
Matematiškai dispersija nėra tokia sudėtinga:
- Apskaičiuokite reikšmių aibės vidurkį. Norėdami apskaičiuoti vidurkį, paimkite visų reikšmių sumą, padalytą iš verčių skaičiaus.
- Paimkite kiekvieną savo rinkinio vertę ir atimkite ją iš vidurkio.
- Padėkite gautas reikšmes kvadratu (kad panaikintumėte neigiamus skaičius).
- Sudėkite visas kvadratines vertes kartu.
- Apskaičiuokite kvadratinių verčių vidurkį, kad gautumėte dispersiją.
Taigi, kaip matote, tai nėra sunku apskaičiuoti. Tačiau, jei turite šimtus ar tūkstančius reikšmių, tai užtruks amžinai, kad tai padarytumėte rankiniu būdu. Taigi gerai, kad „Excel“ gali automatizuoti procesą!
Kam naudojate dispersiją?
Pats dispersija turi daugybę naudojimo būdų. Žvelgiant vien iš statistinės perspektyvos, tai geras trumpas būdas išreikšti duomenų rinkinio paskirstymą. Investuotojai naudoja dispersiją, kad įvertintų tam tikros investicijos riziką.
Pavyzdžiui, įvertinę akcijų vertę per tam tikrą laikotarpį ir apskaičiavę jos dispersiją, gausite gerą supratimą apie jos kintamumą praeityje. Darant prielaidą, kad praeitis numato ateitį, tai reikštų, kad kažkas su maža dispersija yra saugesnis ir labiau nuspėjamas.
Taip pat galite palyginti kažkokius skirtumus skirtingais laikotarpiais. Tai gali padėti nustatyti, kada kitas paslėptas veiksnys daro įtaką kažkam, keičia jo dispersiją.
Variacija taip pat yra stipriai susijusi su kita statistika, žinoma kaip standartinis nuokrypis. Atminkite, kad vertės, naudojamos dispersijai apskaičiuoti, yra kvadratinės. Tai reiškia, kad dispersija neišreiškiama tuo pačiu pradinės vertės vienetu. Standartiniam nuokrypiui reikia paimti kvadratinę dispersijos šaknį, kad vertė būtų grąžinta į pradinį vienetą. Taigi, jei duomenys buvo kilogramais, tada standartinis nuokrypis taip pat yra.
Pasirinkimas tarp populiacijos ir imties dispersijos
„Excel“ yra du dispersijos potipiai su šiek tiek skirtingomis formulėmis. Kurį pasirinkti, priklauso nuo jūsų duomenų. Jei jūsų duomenys apima visą „populiaciją“, turėtumėte naudoti populiacijos dispersiją. Šiuo atveju „populiacija“ reiškia, kad jūs turite visas vertybes kiekvienam tikslinės gyventojų grupės nariui.
Pavyzdžiui, jei žiūrite į kairiarankių žmonių svorį, tada į populiaciją įeina kiekvienas kairiarankis žmogus Žemėje. Jei pasvėrėte juos visus, naudotumėte populiacijos dispersiją.
Žinoma, realiame gyvenime dažniausiai pasitenkiname mažesne imtimi iš didesnės populiacijos. Tokiu atveju turėtumėte naudoti imties dispersiją. Populiacijos dispersija vis dar praktiška mažesnėms populiacijoms. Pavyzdžiui, įmonėje gali būti keli šimtai ar keli tūkstančiai darbuotojų, turinčių duomenis apie kiekvieną darbuotoją. Jie atstovauja „populiacijai“ statistine prasme.
Tinkamos dispersijos formulės pasirinkimas
Programoje „Excel“ yra trys imties dispersijos formulės ir trys populiacijos dispersijos formulės:
- VAR , VAR.S ir VARA imties dispersijai.
- VARP , VAR.P ir VARPA populiacijos dispersijai.
Galite nepaisyti VAR ir VARP. Jos yra pasenusios ir skirtos tik suderinamumui su senomis skaičiuoklėmis.
Belieka VAR.S ir VAR.P, kurios skirtos skaitinių reikšmių rinkinio dispersijai apskaičiuoti, ir VARA ir VARPA, kurios apima teksto eilutes.
VARA ir VARPA konvertuos bet kurią teksto eilutę į skaitinę reikšmę 0, išskyrus „TRUE“ ir „FALSE“. Jie atitinkamai konvertuojami į 1 ir 0.
Didžiausias skirtumas yra tas, kad VAR.S ir VAR.P praleidžia visas neskaitines reikšmes. Tai reiškia, kad šie atvejai neįtraukiami į bendrą reikšmių skaičių, o tai reiškia, kad vidutinė reikšmė skirsis, nes padalijate iš mažesnio atvejų skaičiaus, kad gautumėte vidurkį.
Kaip apskaičiuoti dispersiją „Excel“.
Viskas, ko jums reikia norint apskaičiuoti dispersiją programoje „Excel“, yra reikšmių rinkinys. Toliau pateiktame pavyzdyje naudosime VAR.S, tačiau formulė ir metodai yra visiškai tokie patys, neatsižvelgiant į tai, kurią dispersijos formulę naudojate:
- Darant prielaidą, kad turite paruoštą diapazoną arba atskirą reikšmių rinkinį, pasirinkite tuščią pasirinktą langelį .
- Formulės lauke įveskite =VAR.S(XX:YY) , kur X ir Y reikšmės pakeičiamos pirmuoju ir paskutiniu diapazono langelių numeriais.
- Paspauskite Enter , kad užbaigtumėte skaičiavimą.
Arba galite nurodyti konkrečias reikšmes. Tokiu atveju formulė atrodo taip =VAR.S(1,2,3,4) . Skaičiai pakeičiami bet kokiais, kurių reikia dispersijai apskaičiuoti. Galite rankiniu būdu įvesti iki 254 reikšmių, tačiau, nebent turite tik keletą reikšmių, beveik visada geriau įvesti duomenis langelių diapazone ir tada naudoti pirmiau aptartos formulės langelių diapazono versiją.
Galite Excel adresu, Er, Excel
Dispersijos skaičiavimas yra naudingas triukas, kurį reikia žinoti visiems, kuriems reikia atlikti statistinį darbą „Excel“. Bet jei kuri nors iš šiame straipsnyje naudotų „Excel“ terminų buvo paini, apsvarstykite galimybę peržiūrėti „Microsoft Excel“ pagrindų mokymo programą – „Mokymasis naudotis Excel“ .
Kita vertus, jei esate pasirengęs daugiau, peržiūrėkite linijinės regresijos tendencijos linijos pridėjimą prie Excel sklaidos diagramos , kad galėtumėte vizualizuoti dispersiją ar bet kurį kitą duomenų rinkinio aspektą, palyginti su aritmetiniu vidurkiu.
Ar galima nepaisyti dispersijos?
Sklaida yra viena iš naudingiausių tikimybių teorijos ir statistikos įrankių. Jis naudojamas duomenų rinkinio kintamumui matuoti. Tačiau statistikoje dispersijos negalima ignoruoti, nes ji padeda įvertinti duomenų kintamumą ir padaryti svarbias išvadas apie kintamųjų ryšį. Jei nepaisysite dispersijos, galite praleisti svarbią informaciją apie savo duomenis ir gauti klaidinančių rezultatų. Taigi geriausia neignoruoti statistikos skirtumų.
Kaip sukurti išskleidžiamąjį sąrašą programoje „Excel“.
Išskleidžiamojo sąrašo naudojimas programoje „Excel“ gali labai sutrumpinti laiką, kurio gali prireikti įvesti duomenis į skaičiuoklę. Sužinokite, kaip efektyviai sukurti išskleidžiamąjį sąrašą „Excel“.
Kaip sukurti ir naudoti automatinį tekstą „Microsoft Word“.
Tekstų rengyklės nuėjo ilgą kelią nuo devintojo dešimtmečio pradžios, kai „Microsoft“ pirmą kartą išleido „Microsoft Word“, skirtą MS-DOS. Jo novatoriška savybė buvo ta, kad ji buvo sukurta naudoti su pele.
Kaip sukurti Ganto diagramas „Microsoft Excel“.
Ganto diagramos yra populiarus būdas sekti projektus, ypač komandoms, kurioms reikia nepamiršti užduoties trukmės. Veiksmingai naudodami Ganto diagramą galite užtikrinti, kad skirtingos užduotys netrukdytų viena kitai, ir netgi nustatyti, kada viena turi būti baigta, kad galėtų pradėti kitą.
Kaip įterpti parašą į „Microsoft Word“ dokumentą
Štai dažnas scenarijus: el. paštu gavote „Word“ dokumentą, kurį turite pasirašyti ir išsiųsti atgal. Galite atspausdinti, pasirašyti, nuskaityti ir grąžinti dokumentą, bet yra paprastesnis, geresnis ir greitesnis būdas įterpti parašą į Word.
Kaip sukurti etiketes „Word“ iš „Excel“ skaičiuoklės
Jei norite sukurti ir spausdinti bet kokias etiketes, ieškokite tik Microsoft Word ir Excel. Etikečių duomenis galite saugoti programoje „Excel“, o tada gauti tuos duomenis programoje „Word“, kad išsaugotumėte arba atsispausdintumėte etiketes.
Kaip naudoti laiškų suliejimą programoje Word kuriant laiškus, etiketes ir vokus
Laiškų suliejimas yra „Microsoft Word“ funkcija, padedanti supaprastinti suasmenintų laiškų, etikečių, vokų, el. laiškų ir katalogo kūrimą. Kadangi laiškų suliejimas nėra viena iš dažniausiai naudojamų MS Word funkcijų, kai kurie vartotojai gali nežinoti, kaip atlikti laiškų suliejimą programoje Word, kad būtų sukurtos raidės, etiketės ir vokai.
Kaip naudoti „Excel“ automatinio atkūrimo ir automatinio atsarginio kopijavimo funkcijas
Visada yra baisi tragedija, kai kas nors praranda kažką svarbaus, su kuriuo dirbo, nes tinkamai neišsaugojo savo dokumento. Tai nutinka dažniau, nei manote „Excel“ ir „Word“ naudotojams.
Kaip rūšiuoti tekstą programoje Word
Kai dauguma žmonių galvoja apie teksto rūšiavimą programoje, jie galvoja apie langelių rūšiavimą „Excel“ skaičiuoklėje. Tačiau galite rūšiuoti tekstą programoje „Word“, jei yra kažkas, kas nurodo „Word“, kur prasideda ir baigiasi skirtingos teksto dalys.
Kaip sukurti histogramą „Excel“.
Histograma yra diagramos tipas, kurį galite generuoti iš duomenų programoje „Excel“. Tai leidžia lengvai apibendrinti konkrečių verčių dažnumą duomenų rinkinyje.
Kaip sukurti sveikinimo atviruką naudojant MS Word
„Microsoft Word“ gali nuveikti daug daugiau, ne tik ataskaitų ir gyvenimo aprašymų kūrimas. Jame yra tinkamas grafinių įrankių rinkinys, padedantis kurti grafinius dokumentus, pavyzdžiui, sveikinimo atvirukus.
Kaip nustatyti ir naudoti MLA formatą „Microsoft Word“.
Šiuolaikinės kalbos asociacija (MLA) yra organizacija, teikianti gaires profesionaliems ir akademiniams rašytojams. Daugelis universitetų, darbdavių ir profesionalių agentūrų dabar reikalauja, kad rašytojai atitiktų MLA stilių, nes juo lengva naudotis ir jis yra nuoseklus.
Kaip pagal numatytuosius nustatymus išsaugoti „Office“ dokumentus vietiniame kompiuteryje
Pagal numatytuosius nustatymus, jei esate prisijungę prie „Office“ programų naudodami „Microsoft“ paskyrą, jūsų programos išsaugo dokumentus „OneDrive“ saugykloje. Tai skatina saugoti failus debesyje, kad galėtumėte pasiekti tuos failus kituose sinchronizuojamuose įrenginiuose.
Kaip priversti „OneDrive“ nustoti siųsti prisiminimus el. paštu
Jei naudojate „OneDrive“, kad sukurtumėte atsarginę nuotraukų bibliotekos kopiją, ji reguliariai el. paštu siunčia prisiminimus – vaizdus ir vaizdo įrašus iš tos pačios dienos ankstesniais metais. Štai kaip juos išjungti „Windows“, „Android“, „iPhone“ ir „iPad“.
Kaip atidaryti kelis Excel egzempliorius
Jei kada nors dirbote su keliomis darbaknygėmis programoje „Excel“, žinote, kad kartais gali kilti problemų, jei visos darbaknygos yra atidarytos tame pačiame „Excel“ egzemplioriuje. Pavyzdžiui, jei perskaičiuosite visas formules, tai bus daroma visoms atidarytoms darbaknygėms tame pačiame egzemplioriuje.
Kaip spausdinti ant voko „Microsoft Word“.
Jei norite siųsti profesionaliai atrodančią korespondenciją, neleiskite, kad pirmas dalykas, kurį gavėjas pamatytų, būtų netvarkingas ranka rašytas vokas. Paimkite voką, įdėkite jį į spausdintuvą ir naudodami Microsoft Word įveskite pavadinimą bei adresą.
Kaip sukurti pildomas formas Word
Ar žinojote, kad „Word“ galite kurti formas, kurias žmonės gali užpildyti. Kai girdite apie užpildomas formas, tai beveik visada yra susijusi su Adobe ir PDF dokumentais, nes tai yra populiariausias formatas.
Kaip sukurti knygelę Word
„Microsoft Word“ yra būtina visiems, kurie dirba su dokumentais. Žodžiai buvo naudojami taip ilgai, kad be jo neįmanoma įsivaizduoti biuro, mokyklos ar kitokio skaitmeninio darbo.
Kaip įrašyti makrokomandą „Excel“.
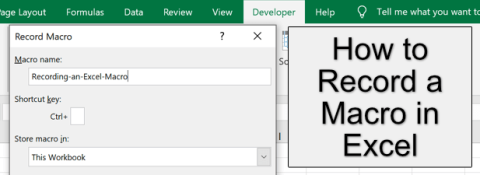
Vėl ir vėl atlikti tuos pačius veiksmus nėra tik nuobodu, bet tai gali būti ir laiko švaistymas bei našumo išeikvojimas. Tai ypač aktualu pradedantiesiems „Excel“ naudotojams, kurie gali nesuprasti, kad įprastas užduotis lengva automatizuoti įrašant makrokomandą.
Kaip rasti ir apskaičiuoti diapazoną programoje „Excel“.
Matematiškai apskaičiuojate diapazoną iš didžiausios tam tikro duomenų rinkinio vertės atėmę mažiausią reikšmę. Tai rodo reikšmių sklaidą duomenų rinkinyje ir yra naudinga matuojant kintamumą – kuo didesnis diapazonas, tuo jūsų duomenys yra labiau išsklaidyti ir kintantys.
🔧 Ištaisykite „Microsoft Edge“ puslapio nereagavimo klaidą 2026 m.: 10 patikrintų žingsnių, kaip akimirksniu atsikratyti problemų!
Pavargote nuo „Microsoft Edge“ puslapio nereagavimo ir naršymo sustabdymo? Vadovaukitės mūsų 2026 m. atnaujintu vadovu, kuriame rasite greitus sprendimus, pvz., skirtukų perkėlimą, talpyklos išvalymą ir plėtinių išjungimą, kad greitai atkurtumėte sklandų veikimą. Nereikia jokių techninių įgūdžių!
Apsaugokite mažuosius tyrinėtojus: išsamus vadovas, kaip naudoti „Microsoft Edge“ vaikų režimą saugesniam naršymui
Atraskite saugesnius internetinius nuotykius savo vaikams naudodami „Microsoft Edge“ vaikų režimą. Žingsnis po žingsnio sąranka, tinkinimo patarimai ir saugos funkcijos naršymui be rūpesčių. Pradėkite saugoti jau šiandien!
Išspręskite „Microsoft Edge Precision“ tvarkyklių suderinamumo problemas dabar – patikrinti pataisymai sklandžiam naršymui!
Išspręskite „Microsoft Edge Precision Driver“ suderinamumo problemas su šiuo išsamiu vadovu. Ištaisykite jutiklinės planšetės slinkties, vėlavimo ir klaidų atsiradimą sistemoje „Windows“, kad veikimas būtų sklandus. Žingsnis po žingsnio sprendimai viduje!
🚨 Ištaisykite „Microsoft Edge“ privataus ryšio įspėjimus per kelias minutes – išsamus 2026 m. vadovas!
Pavargote nuo „Microsoft Edge“ privataus ryšio įspėjimų, blokuojančių jūsų naršymą? Vadovaukitės mūsų patikrintu nuosekliu vadovu, kad greitai ištaisytumėte klaidas „Jūsų ryšys nėra privatus“. Saugūs pataisymai, skirti naujausioms „Edge“ versijoms.
Greitas „Microsoft Edge“ aukščio nustatymo paslaugos išjungimo klaidos ištaisymas – išsamus 2026 m. vadovas
Pavargote nuo erzinančios „Microsoft Edge Elevation Service Disable“ klaidos, blokuojančios atnaujinimus? Vadovaukitės mūsų patikrintais, nuosekliais sprendimais, kad greitai ją išspręstumėte ir atkurtumėte sklandų naršymą. Nereikia jokių techninių žinių!
Atraskite maksimalų produktyvumą: kaip naudoti „Microsoft Edge“ nuotoliniam darbui ir švietimui
Įvaldykite nuotolinį darbą ir mokymąsi naudodami „Microsoft Edge“. Išmokite esminių funkcijų, tokių kaip kolekcijos, įtraukianti skaitytuvė ir „Copilot“ integracija, kad sklandus produktyvumas ir mokymasis būtų kuo geresni. Padidinkite efektyvumą jau šiandien!
🚀 Momentinis pataisymas: kaip ištaisyti „Microsoft Edge MSI“ klaidą 1722 „Windows Installer“ per kelias minutes!
Pavargote nuo „Microsoft Edge MSI“ klaidos 1722, blokuojančios diegimą? Atraskite patikrintus, nuoseklius „Windows Installer“ klaidų taisymus, kad greitai atkurtumėte sklandų naršymą.
🚀 Ištaisykite „Microsoft Edge PowerShell ISE“ klaidą 2026 per kelias minutes – patikrinti 2026 sprendimai!
Kyla problemų dėl „Microsoft Edge PowerShell ISE“ klaidos 2026? Atraskite nuoseklius sprendimus, kurie padės greitai išspręsti šią varginančią problemą. Atnaujinta su naujausiais sklandaus naršymo ir scenarijų kūrimo metodais.
🚀 Momentinis pataisymas: „Microsoft Edge“ negali skaityti arba rašyti į duomenų katalogą, išspręsta per kelias minutes!
Kyla problemų dėl „Microsoft Edge“ klaidos „Negalima skaityti arba rašyti į duomenų katalogą“? Atraskite patikrintus, nuoseklius sprendimus, kaip atkurti sklandų naršymą. Greiti sprendimai „Windows“ naudotojams – nereikia jokių techninių įgūdžių!
🚀 Ištaisykite „Microsoft Edge Untitled“ klaidą kiekvieno paleidimo metu: patikrinti sprendimai, kurie veikia akimirksniu!
Pavargote nuo erzinančios „Microsoft Edge Untitled“ klaidos, dėl kurios naršyklė užstringa paleidžiant? Vadovaukitės mūsų nuosekliu vadovu su greitais pataisymais, kad išspręstumėte problemą visam laikui ir atkurtumėte sklandų naršymą. Atnaujinta su naujausiais „Edge“ pataisymais.