Dakle, od vas se traži da izračunate varijancu pomoću programa Excel, ali niste sigurni što to znači ili kako to učiniti. Ne brinite, to je jednostavan koncept i još lakši proces. Začas ćete postati profesionalac za varijacije!
Što je varijanca?
"Varijanca" je način mjerenja prosječne udaljenosti od srednje vrijednosti. "Prosjek" je zbroj svih vrijednosti u skupu podataka podijeljen s brojem vrijednosti. Varijanca nam daje ideju o tome teže li vrijednosti u tom skupu podataka, u prosjeku, ravnomjerno se pridržavati srednje vrijednosti ili se raspršuju posvuda.

Matematički, varijanca nije tako složena:
- Izračunajte srednju vrijednost skupa vrijednosti. Za izračun srednje vrijednosti uzmite zbroj svih vrijednosti podijeljen s brojem vrijednosti.
- Uzmite svaku vrijednost u svom skupu i oduzmite je od srednje vrijednosti.
- Kvadrirajte dobivene vrijednosti (kako biste poništili negativne brojeve).
- Zbrojite sve vrijednosti na kvadrat.
- Izračunajte srednju vrijednost kvadrata da biste dobili varijancu.
Kao što vidite, vrijednost nije teško izračunati. Međutim, ako imate stotine ili tisuće vrijednosti, bilo bi potrebno zauvijek da to učinite ručno. Dakle, dobro je što Excel može automatizirati proces!
Za što koristite odstupanje?
Varijanca sama po sebi ima brojne namjene. Iz čisto statističke perspektive, to je dobar stenografski način izražavanja koliko je skup podataka raširen. Ulagači koriste varijancu za procjenu rizika danog ulaganja.
Na primjer, uzimajući vrijednost dionice tijekom određenog vremenskog razdoblja i izračunavajući njezinu varijancu, dobit ćete dobru ideju o njezinoj volatilnosti u prošlosti. Pod pretpostavkom da prošlost predviđa budućnost, to bi značilo da je nešto s malom varijancom sigurnije i predvidljivije.
Također možete usporediti varijance nečega u različitim vremenskim razdobljima. To može pomoći u otkrivanju kada drugi skriveni faktor utječe na nešto, mijenjajući njegovu varijancu.
Varijanca je također snažno povezana s drugom statistikom poznatom kao standardna devijacija. Zapamtite da su vrijednosti koje se koriste za izračun varijance kvadratne. To znači da varijanca nije izražena istom jedinicom izvorne vrijednosti. Standardna devijacija zahtijeva uzimanje kvadratnog korijena varijance da bi se vrijednost vratila na izvornu jedinicu. Dakle, ako su podaci bili u kilogramima, onda je i standardna devijacija.
Odabir između populacije i varijance uzorka
Postoje dvije podvrste varijance s neznatno različitim formulama u Excelu. Koji ćete odabrati ovisi o vašim podacima. Ako vaši podaci uključuju cijelu "populaciju", trebali biste koristiti varijancu populacije. U ovom slučaju "populacija" znači da imate svaku vrijednost za svakog člana ciljne skupine stanovništva.

Na primjer, ako gledate težinu ljevorukih ljudi, tada populacija uključuje sve pojedince na Zemlji koji su ljevoruki. Ako ste ih sve izvagali, upotrijebili biste varijancu populacije.
Naravno, u stvarnom životu obično se zadovoljimo manjim uzorkom iz veće populacije. U tom biste slučaju upotrijebili varijancu uzorka. Varijanca u populaciji još uvijek je praktična s manjim populacijama. Na primjer, tvrtka može imati nekoliko stotina ili nekoliko tisuća zaposlenih s podacima o svakom zaposleniku. Oni predstavljaju "populaciju" u statističkom smislu.
Odabir prave formule varijance
U programu Excel postoje tri formule varijance uzorka i tri formule varijance populacije:
- VAR , VAR.S i VARA za varijancu uzorka.
- VARP , VAR.P i VARPA za varijancu populacije.
Možete zanemariti VAR i VARP. Oni su zastarjeli i dostupni su samo radi kompatibilnosti s naslijeđenim proračunskim tablicama.
To ostavlja VAR.S i VAR.P, koji služe za izračunavanje varijance skupa numeričkih vrijednosti i VARA i VARPA, koji uključuju tekstualne nizove.

VARA i VARPA pretvorit će bilo koji tekstualni niz u brojčanu vrijednost 0, s izuzetkom "TRUE" i "FALSE". Oni se pretvaraju u 1 odnosno 0.
Najveća je razlika u tome što VAR.S i VAR.P preskaču sve nenumeričke vrijednosti. Ovo isključuje te slučajeve iz ukupnog broja vrijednosti, što znači da će srednja vrijednost biti drugačija, jer dijelite s manjim brojem slučajeva da biste dobili srednju vrijednost.
Kako izračunati varijancu u Excelu
Sve što trebate za izračunavanje varijance u Excelu je skup vrijednosti. Koristit ćemo VAR.S u primjeru u nastavku, ali formula i metode potpuno su iste bez obzira na to koju formulu varijance koristite:
- Pod pretpostavkom da imate spreman raspon ili diskretni skup vrijednosti, odaberite praznu ćeliju po svom izboru.
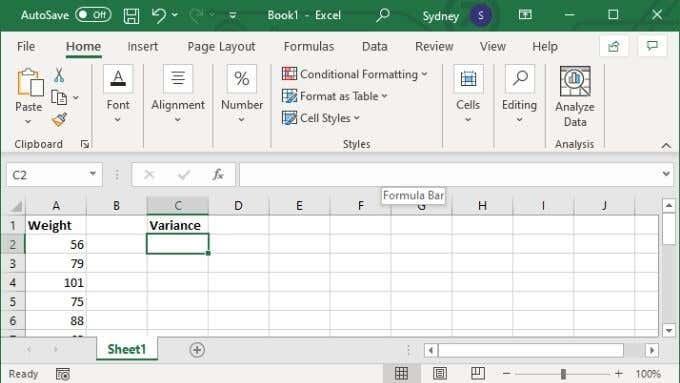
- U polje formule upišite =VAR.S(XX:YY) gdje su vrijednosti X i Y zamijenjene prvim i zadnjim brojevima ćelija u rasponu.
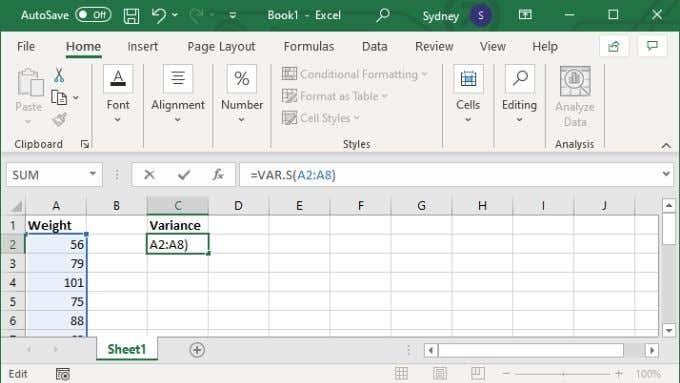
- Pritisnite Enter za dovršetak izračuna.
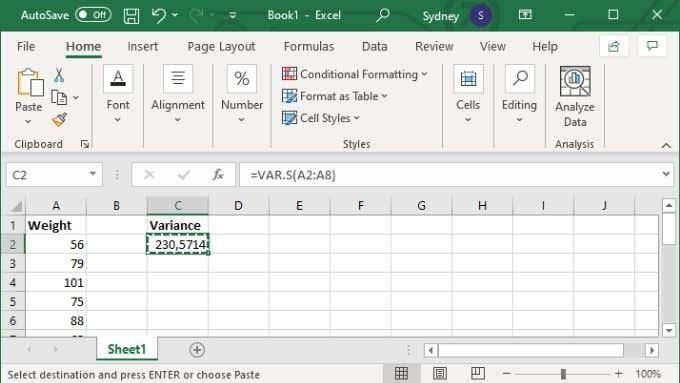
Alternativno, možete odrediti određene vrijednosti, u kojem slučaju formula izgleda kao =VAR.S(1,2,3,4) . S brojevima zamijenjenim onim što vam je potrebno za izračun varijance. Na ovaj način možete ručno unijeti do 254 vrijednosti, ali osim ako nemate samo nekoliko vrijednosti, gotovo je uvijek bolje unijeti podatke u raspon ćelija, a zatim upotrijebiti verziju formule za raspon ćelija o kojoj smo govorili gore.
Možete Excel u, Er, Excel
Izračunavanje varijance koristan je trik za svakoga tko treba obaviti neki statistički rad u Excelu. Ali ako je bilo koja terminologija programa Excel koju smo koristili u ovom članku bila zbunjujuća, razmislite o tome da pogledate Vodič za osnove Microsoft Excela – Učenje korištenja Excela .
Ako ste, s druge strane, spremni za više, pogledajte Dodavanje crte trenda linearne regresije u dijagram raspršenosti programa Excel kako biste mogli vizualizirati varijancu ili bilo koji drugi aspekt skupa podataka u odnosu na aritmetičku sredinu.
Može li se varijanca zanemariti?
Varijanca je jedan od najkorisnijih alata u teoriji vjerojatnosti i statistici. Koristi se za mjerenje varijabilnosti skupa podataka. Međutim, varijanca se ne može zanemariti u statistici jer pomaže u procjeni varijabilnosti podataka i izvlačenju važnih zaključaka o odnosu između varijabli. Ako zanemarite varijancu, mogli biste propustiti važne informacije o svojim podacima i dovesti do pogrešnih rezultata. Stoga je najbolje ne zanemariti odstupanja u statistici.